APOYO TEST GRADO QUINTO 1

APOYO TEST GRADO QUINTO 1 from Carlos Campaña Montenegro

EDUCADOR, ESCRITOR Y CONFERENCISTA KEN ROBINSON

EDUCADOR, ESCRITOR Y CONFERENCISTA KEN ROBINSON de Carlos Campaña Montenegro

MATERIAL PARA NIÑOS PREESCOLAR

MATERIAL PARA NIÑOS PREESCOLAR from Carlos Campaña Montenegro

JUEGO MATEMÁTICO PARA LA FAMILIA ESTRELLA CHINA

JUEGO MATEMÁTICO PARA LA FAMILIA ESTRELLA CHINA

MATERIALES:

• Cartón, cartulina, cartón paja, MDF, etc.
• vinilos
• Lápiz
• Borrador
• Tijeras
• fichas de parques

ELABORACIÓN DEL TABLERO

Necesitamos un cuadrado de 38 centímetros x 38 centímetros.

copiaremos el patrón ampliándolo en una cartulina o en un cartón.

Una opción en MDF es realizar en cada punto un agujero, si se tiene los materiales es una excelente opción.

DINÁMICA DEL JUEGO

1-Consta de un tablero en forma de Estrella de 6 puntas.

2-Cada punta tiene 10 agujeros, a los que corresponde igual cantidad de fichas de un mismo color

3-Se puede jugar entre 2 a 6 jugadores simultáneamente.

4- consiste en mover tus 10 fichas de una punta a la opuesta, ganando el primero en obtenerlo.

Inicio del juego para dos jugadores.

Que movimientos son posibles realizar y cuales no:

• Las piezas pueden moverse a cualquiera de 6 casillas adyacentes vacías.
• Si la casilla a la que quiere mover está ocupada (ya sea por fichas del mismo color -piezas propias- o por fichas de colores distintos -piezas rivales) la pieza puede SALTAR estas fichas y moverse a la primera casilla libre en la dirección lineal del salto.
• Se puede concatenar una cadena de saltos. Es decir, si tras el primer salto -según lo comentado en el punto anterior- existe la posibilidad de realizar otro salto incluso cambiando de dirección, la pieza puede realizar ese nuevo salto si así lo desea… y así sucesivamente.
• Si tras el segundo salto existe la posibilidad de hacer un tercero, es posible continuar ese salto en la cadena de movimientos hasta que un salto NO sea una opción posible.
• En este juego no es como en las damas, las fichas del contrario NO SE COMEN, se dejan en el tablero.
• No se puede saltar sobre dos fichas continuas, siempre debe existir un espacio vacío.

Ejemplos de movimientos:

La ficha roja puede realizar movimientos a los lugares indicados con los pequeños círculos azules.

La ficha señalada con el circulo rojo realiza tres saltos, llegando al lugar que indica la flecha.

Realización de dos saltos sobre las fichas propias.

Realización de tres saltos sobre las fichas contrarias.

Movimiento no permitido

BENEFICIOS DEL JUEGO

• Práctica de la observación
• Es un juego de tácticas y estrategia.
• Mejora la concentración, el estar pendiente de los movimientos propios y de los contrarios.
• Trabajo de valores como la honestidad, la tolerancia y el respeto a los demás.
• Respeto de normas o reglas propias del juego.
• Refuerzo de la autoestima. Por todas las habilidades y destrezas comentadas, así como por la autonomía personal que se desarrolla en todos los pasos se trata de un juego que beneficia la confianza en las propias capacidades.

HABILIDADES MATEMÁTICAS QUE SE TRABAJAN

• La capacidad de análisis de una situación.
• La estrategia que debemos seguir.
• La evaluación de tus condiciones y recursos.
• El riesgo que se debe asumir para ganar la partida.
• Resolución de problemas
• Visión espacial
• Conceptos geométricos básicos: discriminación de formas, líneas rectas, diagonales.

INFORMACION HISTÓRICA DEL JUEGO

los alemanes fueron sus inventores, quienes en principio le llamaron STERN HALMA (Estrella Halma) haciendo referencia al juego americano que les inspiro y a la forma de estrella de David del tablero.

Cuando llego a los Estados Unidos, ello fueron los que le llamaron “Chinese Checkers” (Damas Chinas) para darle un nombre más exótico.

Utilizaron para su comercialización inicial, decoraciones chinas tales como el famoso dragón chino.

JUEGO MATEMÁTICO TORRES DE HANOI.

JUEGO MATEMÁTICO TORRES DE HANOI

El juego matemático de las Torres de Hanoi consta de tres varillas verticales A, B y C y un número variable de discos. Los discos son todos de diferente tamaño y, en la posición de partida del juego, todos los discos están colocados en la varilla A ordenados de mayor a menor tamaño, esto es, el mayor en el lugar más bajo y el menor arriba.

DINÁMICA DEL JUEGO

1. Comenzando en la posición de partida.

2. Trasladar todos los discos a la varilla B o C se debe definir a que varilla se quiere que sean trasladados, pero colocados también de mayor a menor, en el mismo orden en el que estaban colocados en la varilla A.

 3. Para el traslado de discos podemos utilizar la varilla C, pero se debe cumplir siempre la condición de que sólo se puede mover un disco cada vez y que en ningún caso y en ningún paso se podrá colocar un disco de mayor tamaño sobre otro de menor que él.

4. Del número de discos depende la complejidad de la solución.

¿Cuántos movimientos son necesarios para trasladar los discos de A a C con las condiciones exigidas?

Resolución: recordemos las condiciones:

Caso 1: Para un disco en la varilla A:

Solución: Un movimiento.

Caso 2: Para dos discos en la varilla A:

Solución: Tres movimientos.

Caso 3: Para tres discos en la varilla A.

Solución: Siete movimientos.

Caso 4: Para cuatro discos en la varilla A.

Solución: quince movimientos.

BENEFICIOS DEL JUEGO

• Seguimiento de instrucciones visuales, diferenciación de tamaños.
• Trabajo de la perseverancia en la búsqueda de la solución. Sabemos que ésta existe y eso provoca en nosotros el deseo de conseguirla, pero para ello habrá que perseverar.
• Al tratarse de un juego íntegramente manipulativo y donde no quedan huellas de nuestros intentos podemos probar tantas veces como necesitemos. Si pensamos que una pieza irá en un sitio la colocamos, luego la segunda y la tercera hasta conseguirlo.
• Práctica con la auto corrección.
• Refuerzo de la autoestima. Por todas las habilidades y destrezas comentadas, así como por la autonomía personal que se desarrolla en todos los pasos se trata de un juego que beneficia la confianza en las propias capacidades.

HABILIDADES MATEMÁTICAS QUE SE TRABAJAN

• Resolución de problemas
• Visión espacial
• Razonamiento geométrico
• Conceptos geométricos básicos: discriminación de tamaños, radio de circunferencia.
• Conceptos: mayor que, menor que, arriba, abajo.

PROPUESTA PARA TRABAJAR CON LOS NIÑOS:

• Trabajar con números
•  Nunca un número mayor puede estar arriba de una cantidad menor. 

• Trabajar figuras geométricas.

Llevar las fichas desde el circulo al triángulo.

Llevar las fichas desde el circulo al rectángulo.

• Trabajar con letras

Otra propuesta es recortar trozos de madera y realizar la actividad sin la utilización de varillas, dibujar figuras geométricas en un plano y llevar los trozos de madera de un cuadro a otro

Las medidas son opcionales.

IMPORTANCIA DELA ORTOGRAFÍA

IMPORTANCIA DE LA ORTOGRAFÍA from Carlos Campaña Montenegro

JUEGO DE LÓGICA PARA NIÑOS LLEGAR A MIL

JUEGO DE LÓGICA PARA NIÑOS LLEGAR A MIL

ELABORACIÓN DEL TABLERO

Necesitamos un rectángulo de 27 centímetros x 18 centímetros.

DINÁMICA DEL JUEGO

 1.Este es un juego donde participan dos jugadores.

2.cada jugador lanza un dado, inicia el juego aquel jugador que obtenga el puntaje más alto.

3.Se ubican las fichas en el lugar de inicio (Amarillo).

4. se lanzan los dados:

          No es necesario sacar pares para iniciar el juego.

          Mover en cada ficha el valor obtenido 

OPCIÓN MOVIMIENTO 1

OPCIÓN MOVIMIENTO 2

5.se tiene que llegar exactamente a 10 y se ubica la ficha en el lugar de inicio de las decenas, cuando en esta columna se llegue exactamente a 10 pasa al inicio de la siguiente columna (centenas).

6.la idea es llegar con la totalidad de las fichas al final de la columna de las centenas.

7.Quien llegue primero con sus tres fichas sumara 3000 puntos y el otro jugador sumara según la posición final de sus fichas en ese momento.

* Se juega por turnos, el que tiene el turno lanza los dados, el valor obtenido en estos, es la cantidad de casillas que el jugador puede mover las fichas que tenga en juego en el tablero, en recorrido hacia la meta (unidades, decenas, centenas). Al obtener un par contrario al parques el jugador no tiene derecho a repetir su turno, ademas no hay capturas, ni se sopla por la equivocacion que pueda tener alguno de los jugadores.

TÁCTICAS BÁSICAS

Todas estas tácticas se aprenden y perfeccionan con la práctica. Obviamente, no es una lista exhaustiva. Además, el resultado de estas tácticas depende del estado actual del juego, de la suerte y de la habilidad de los oponentes.

BENEFICIOS DEL JUEGO

• Práctica de la observación y atención ya que se debe mirar que puntaje se obtiene en los dados y que el mismo sea el que se mueve en el tablero.
• Este es un juego que permite mucho el compartir momentos con la familia.
• Los juegos de mesa posibilitan el desarrollo de habilidades cognitivas y lógicas.
• Tienen varias facilidades: se pueden cargar para todas partes, es un juego económico y práctico que lo puede elaborar uno mismo con poco material, el tablero inicial está planteado para dos jugadores, pero al final aparece una propuesta de un tablero para cuatro integrantes.
• Es un juego que permite despojarse del rol de mamá, papá o hijo, y entrar en un mundo mágico donde, más allá del papel que tiene cada uno en el hogar, todos responden a reglas, de una manera intencional.
• En este sentido, existe la posibilidad de que, tanto padres como hijos, asuman un rol, manifiesten su inconformismo o sus acuerdos, planeen estrategias, establezcan límites y reglas, generen nuevos pensamientos, afiancen vínculos, etc. Es decir, que desarrollen todo este tipo de comportamientos, que les servirán para modelar su carácter y personalidad en el futuro.
• Otro aspecto muy importante es que este tipo de juegos le permiten al niño entender y ponerse en los zapatos del otro. Pensar como el otro pensaría, y actuar en consecuencia. Entonces, es muy útil para que los pequeños se vuelvan críticos frente a su manera de actuar y frente a la de los demás.
• Así mismo, existe la posibilidad de desarrollar la habilidad de la tolerancia a la frustración, porque en todo juego hay que ganar o perder, y en estas dinámicas es más visible el manejo de las emociones, los comportamientos y las reacciones frente al triunfo o la derrota.
• Desde el punto de vista cognitivo, favorecen la concentración, la atención, la memoria, el desarrollo de la imaginación, la creatividad.

HABILIDADES MATEMÁTICAS QUE SE TRABAJAN

• Resolución de problemas
• Calculo matemático
• Razonamiento
• Ubicación espacial: arriba, abajo, derecha, izquierda
• Trabajo de columnas y filas.
• Juego de estrategia.

RECOMENDACIONES FINALES

• Este es un juego recomendado para niños mayores de 5 años.
•  Diseñar un tablero que llame la atención.
• Buscar variantes que permitan explorar otros aspectos dentro del juego.
• Aumentar el numero de columnas para incluir unidades de mil, decenas de mil, etc.
• Aumentar el numero a conseguir con lo cual se tendría que jugar mas encuentros: llegar a 6000, 7000, etc… mediante acuerdo de los jugadores.

PROPUESTA DE TABLERO PARA CUATRO JUGADORES

EJEMPLO DE MOVIMIENTOS INICIALES DEL JUEGO

CUENTO PARA NIÑOS QUINO Y DINO

CUENTO PARA NIÑOS QUINO Y DINO from Carlos Campaña Montenegro

CUBOS PARA CREAR CUENTOS

CUBOS PARA CREAR CUENTOS from Carlos Campaña Montenegro

JUEGO DE LÓGICA PARA NIÑOS CERCAR LOS ARBOLES

 JUEGO DE LÓGICA PARA NIÑOS CERCAR LOS ARBOLES

MATERIALES

• Tapas de gaseosa
• lápiz
• regla
• borrador
• tijeras
• Cartulina, cartón, hoja de bloc, etc.

ELABORACIÓN DEL TABLERO 

Necesitamos dos cuadrados de 16 centímetros x 16 centímetros.

Con uno de ellos elaboramos el tablero de juego.

Con el segundo tablero recortamos las cercas o vallas.

DINÁMICA DEL JUEGO 

1.Se escoge un reto(patrón).

2.Se colocan los arboles (tapas de gaseosa) tal y como indica el reto. Hay que colocar el tablero siempre en una posición determinada, como se ve en el reto.

3.Ahora empieza el desafío: se trata de colocar las cercas en el tablero dejando a los arboles fuera de ellas.

4. Siempre las tres cercas (vallas) deben ubicarse en el tablero.

BENEFICIOS DEL JUEGO

• Práctica de la observación ya que desde la colocación de los elementos que intervendrán en el reto hasta la resolución necesita de la mirada atenta.
• Seguimiento de instrucciones visuales. En el planteamiento del reto no hay información verbal ni escrita, tan sólo gráfica. Se trata de un problema de tipo visual.
• Trabajo de la perseverancia en la búsqueda de la solución. Sabemos que ésta existe y eso provoca en nosotros el deseo de conseguirla, pero para ello habrá que perseverar.
• Familiarización del método de tanteo y acierto-error. Al tratarse de un juego íntegramente manipulativo y donde no quedan huellas de nuestros intentos podemos probar tantas veces como necesitemos. Si pensamos que una pieza irá en un sitio la colocamos, luego la segunda y  la tercera .Exploramos cambiando de lugar las vallas.
• Práctica con la auto corrección. Todos los retos tienen su solución al final
• Refuerzo de la autoestima. Por todas las habilidades y destrezas comentadas, así como por la autonomía personal que se desarrolla en todos los pasos se trata de un juego que beneficia la confianza en las propias capacidades.

HABILIDADES MATEMÁTICAS QUE SE TRABAJAN

• Resolución de problemas
• Visión espacial
• Razonamiento geométrico
• Conceptos topológicos 
• Conceptos geométricos básicos: discriminación de formas, cuadrado, círculos, líneas rectas, ángulos.

RECOMENDACIONES FINALES

• El juego de lógica cercar los arboles es adecuado para niños de cuatro años en adelante. Quizá el límite de edad sea más por la temática que por la dificultad del juego. Recomendado para niños de 4 a 8 años.
•  Plastificar los retos o desafíos para una mayor duración.
• Los retos pueden ser impresos, o elaborados de manera manual.
• Si quieren llamar más la atención del niño utilizar pequeñas figuras y el reto viene planteado que tiene que encerrar dichas figuras (carros, dinosaurios, muñecos, etc.) 

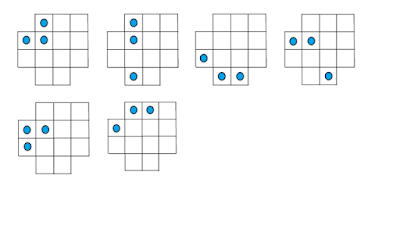
RETOS O PATRONES

EJEMPLO CON LA SOLUCIÓN CORRESPONDIENTE

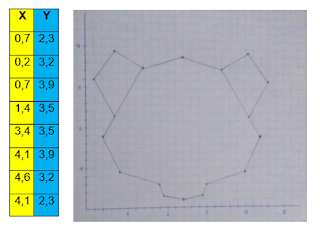
DIBUJO OSO PANDA GEOMÉTRICO MATEMÁTICO

DIBUJO OSO PANDA GEOMÉTRICO MATEMÁTICO

MATERIALES PARA ESTE PROYECTO

Es importante tener el patrón o figura guía para observar como poco a poco va quedando nuestro proyecto. 

La parte mas sencilla de trabajar es el contorno de la cabeza.

Enseguida trabajamos las orejas

Continuamos con los ojos

la nariz

Y finalmente los puntos claves para poder terminar esta hermosa figura.

Es recomendable pintar de color negro:

• orejas
• ojos
• nariz
• boca

Dibujo geométrico

Geométrico es aquello vinculado a la geometría, que es la especialidad de las matemáticas orientada al análisis de las magnitudes y las propiedades de las figuras en el espacio o en un plano. Un dibujo geométrico, por lo tanto, es aquel que se realiza siguiendo las reglas de esta disciplina.

Estos gráficos se llevan a cabo mediante figuras planas, las cuales se construyen siguiendo un método lógico. Por lo general se apela a ciertos trazados básicos (triángulos, círculos, cuadrados, etc.) para el desarrollo de los dibujos.

Los dibujos geométricos pueden emplearse con distintos fines. En ocasiones se trata de dibujos artísticos que buscan generar determinados efectos ópticos. En este caso, se privilegia el resultado estético. También hay dibujos geométricos que desarrollan los profesionales en el marco de otras clases de dibujos (como un arquitecto que recurre a un rectángulo para representar una habitación en un plano). Los niños, por otro lado, pueden aprender a reconocer las diversas figuras de la geometría e incluso a colorear a través de los dibujos geométricos.

Existen diversas maneras de realizar estos dibujos. Pueden hacerse sobre un papel, un cartón u otra superficie plana, a mano y con ayuda de algún instrumento (una regla, una escuadra, un compás u otro), por ejemplo.